The basic technique of most trees(Binary) uses the concept of DFS or BFS.
The order of which we explore a three determines if its
PRE_ORDER,POST_ORDER,IN_ORDER. I assume this concepts is all about doing same thing in ONLY 3 STEPS.
- VISIT ROOT - VISIT LEFT - VISIT RIGHT
- VISIT LEFT - VISIT ROOT - VISIT RIGHT
- VISIT RIGHT - VISIT LEFT - VISIT ROOT
The order of which this visit is done determines if its pre-order,post-order or inorder traversal.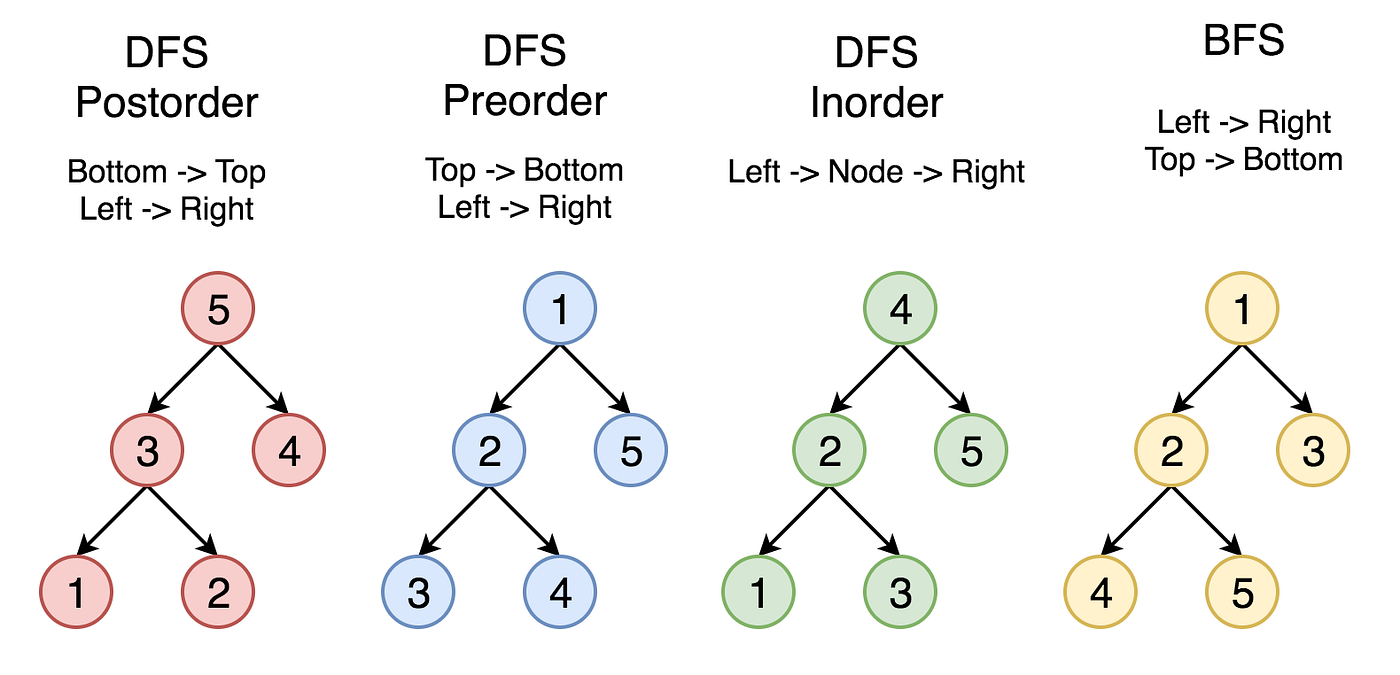
Problem Analysis
In the Path sum problem all we need to do is check if the path from the root to the
leaf node makes up the sum of the target sum value.
But how do we get to the leaf node of a tree and also keep track of the nodes we visited already?
We go in depth
Always go too far, because that's where you'll find the truth.
— Albert Camus
If that clicks enough for a clue. It implies we need to do a depth first search(DFS↡).
In this example I would try to use an easier way to implement that(a recursion ₪₪).
The go is to go indepth from each node. which implies we keep going left of node.
Well if there is no right we return to the call stack and start exploring the
right of the call stack. In this order we can get to all the leaf nodes.
What happens at the leaf node and how do we know?
A leaf node is just a node with NO LEFT NODE and RIGHT NODE.
If we actually traveled to the leaf node, then what relation does it have with the targetSum?
Well, it implies if we subtract all values of nodes visited before the leaf NODE,
then the targetSum remainder value should be equal to the leaf node value.
If it IS NOT, it means the path does not sum to the target. We can check else where.
Code Implementation
lets declare our result as global
List<List<Integer>> res= new ArrayList<>();Let's check where the leaf node is.
if(root.left==null && root.right==null && targetSum==root.val)res.add(new ArrayList<>(stkTrack));We can just embed it in our recursive helper function.
private void getPathSum(TreeNode root, int targetSum, Stack<Integer> stkTrack) {
stkTrack.push(root.val);
//The root val can only be same as the targetSum if after substraction all the previous values
// the remaining is same as the value of the last(leaf) node
if(root.left==null && root.right==null && targetSum==root.val)res.add(new ArrayList<>(stkTrack));
if(root.left!=null)getPathSum(root.left,targetSum-root.val,stkTrack);
if(root.right!=null)getPathSum(root.right,targetSum-root.val,stkTrack);
stkTrack.pop();
}In our main pathSum function we can just use the above function
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
if(root==null)return res;
Stack<Integer> stkTrack = new Stack<>();
getPathSum(root,targetSum,stkTrack);
return res;
}Summary
Don't forget how we kept subtraction each root value from the targetSum or each call
if(root.left!=null)getPathSum(root.left,targetSum-root.val,stkTrack);
if(root.right!=null)getPathSum(root.right,targetSum-root.val,stkTrack);Also observe how the stack removes element from the stack if all the above three conditions fails.
if(root.left==null && root.right==null && targetSum==root.val)res.add(new ArrayList<>(stkTrack));
if(root.left!=null)getPathSum(root.left,targetSum-root.val,stkTrack);
if(root.right!=null)getPathSum(root.right,targetSum-root.val,stkTrack);
//here
stkTrack.pop();If we added a value from the tree, and its leaf but does not sum to target, it implies
all the above conditions are going to fail. so we remove it from our stack.
Remember the call stack would return to the previous node and check if that node has left node
or right node. and it continues
Same Question with little twist
Just copy+paste your solution with just condition check on return
path-sum-ii
path-sum
'Algorithm' 카테고리의 다른 글
| 1448.(BINARY TREE) Count Good Nodes 🌳 (0) | 2022.09.01 |
|---|---|
| Topological Sorting (0) | 2022.08.30 |
| What is Big O ? (0) | 2022.08.24 |
| Leetcode 37. Sudoku Solver (Hard) (0) | 2022.08.24 |
| 102. Binary Tree Level Order Traversal (0) | 2022.07.14 |