Initially when you read the question.What first came to mind could be using "Two Heaps" approach.
How would Two Heaps work?
If the numbers and the multipliers are kept in two maximum heap and we continuously poll(remove) from the heaps
we can perform multiplication operations until the heaps of numbers is multipliers is empty.
public int maximumScoreTwoHeaps(int[] nums, int[] multipliers) {
PriorityQueue<Integer> numMH= new PriorityQueue<>((x, y) -> Integer.compare(y, x));
PriorityQueue<Integer> multipliersMH= new PriorityQueue<>((x, y) -> Integer.compare(y, x));
for (int n : nums) {
numMH.add(n);
}
for (int n : multipliers) {
multipliersMH.add(n);
}
int score=0;
while (!multipliersMH.isEmpty()){
int x= multipliersMH.poll();
int y= numMH.poll();
score+=(x*y);
}
return score;
}
@Test
public void maximumScoreTwoHeapsTest(){
assertEquals(14,maximumScoreTwoHeaps(new int[]{3,2,1},new int[]{1,2,3}));
}This is because in the question we know multipliers always has the smallest length.
This could be rational if the arrays has no mixture of positive and negative numbers.
But if we have a multiplication of positive and negative numbers then our sum at some point would decrease or increase.
This implies we cannot use two heaps.
What if we have the numbers sorted in descending order?
The problem could be that the maximum of multipliers might number get to the maximum value of nums.
Because the length is not same.
OR The multiplication of any two negatives that can produce maximum value might be missed out.
Finally, what works
In the case we know that in each operation all we want to do is obtain the possible maximum multiplication of
the i'th item with multipliers. so what can we do?
we can constantly check for only the possible maximum if we multiply from left or right.
In this case we start with memo to keep record of the updates in maximum we obtain.
L denotes the starting index and it goes till the length of multipliers.
So all we need to do is check the point where multipliers are all done.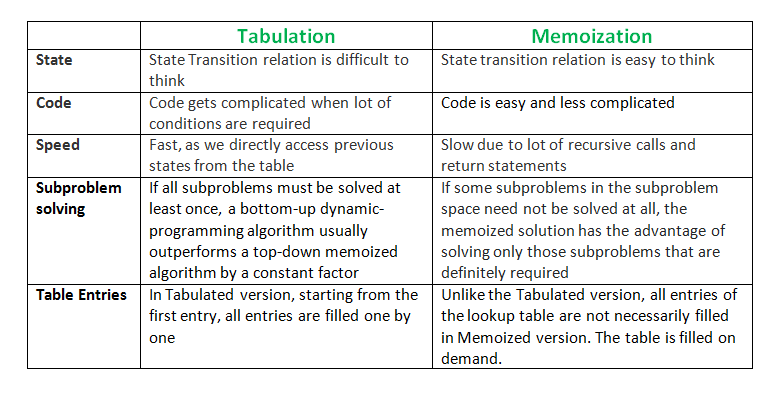
if(L == multipliers.length)
return 0;But we need to make sure the memo we are using is set to 0 or null before we can update it.
we dont want to repeat an update for previous values
if (dp[R][L] != 0)
return dp[R][L];How we are going from Left and Right
int lf = nums[R] * multipliers[L] + memo(nums, multipliers, L + 1, R + 1, N, dp);
int rg = nums[N] * multipliers[L] + memo(nums, multipliers, L + 1, R, N - 1, dp);lf- is the left operations when L[0...M] the length of multipliers
and we move numbers from R[0...R+1..M]
R- is the right operations N[nums.length - 1....M] it means it starts from the end of nums and perform operations
until all the multipliers are done. so we keep decreasing.
Why it is possible??
Because in all operations we just need the maximum of the operation if we multiple nums to the end value or the starting
value of multipliers.
So in the end we obtain the maximum from the left and right operations.
Which is stored in our memo. at the end we obtain the last value of our 2d table which is going to be the sum
at R,L formed from our recursive memory stack callback.
Final Code.
public int maximumScore(int[] nums, int[] multipliers) {
int[][] dp = new int[1000][1000];
return memo(nums, multipliers, 0, 0, nums.length - 1, dp);
}
private int memo(int[] nums, int[] multipliers, int L, int R, int N, int[][] dp) {
if (L == multipliers.length)
return 0;
if (dp[R][L] != 0)
return dp[R][L];
int lf = nums[R] * multipliers[L] + memo(nums, multipliers, L + 1, R + 1, N, dp);
int rg = nums[N] * multipliers[L] + memo(nums, multipliers, L + 1, R, N - 1, dp);
dp[R][L] = Math.max(lf, rg);
return dp[R][L];
}Summary
Always check what is the simplest possible way around a problem.
I still think developing a good recursive function could be hard sometimes. It takes time
'Algorithm' 카테고리의 다른 글
| What is TreeMap in Java (0) | 2022.10.07 |
|---|---|
| 718. Maximum Length of Repeated Subarray (0) | 2022.09.21 |
| 1457. Pseudo-Palindromic Paths in a Binary Tree (0) | 2022.09.14 |
| [리트코드] Remove Duplicates(중복 제거) (0) | 2022.09.02 |
| 1448.(BINARY TREE) Count Good Nodes 🌳 (0) | 2022.09.01 |